平均にひと手間加えて統計的に分析する方法
Table of Contents
統計的推計を業務内で何度か試す機会があったのですが、ある程度知見も溜まってきたので、共有しておきたいと思います。(以前読んだ本のまとめとして……)
平均だけで良いのか #
「最強の学問は統計学である」(西内啓)の書籍の中では、「平均」は19世紀の統計学者がやる集計だと言っていました(たしか)。ちょっとひと手間加えるだけで、統計的な推計ができるようになるので、データへの信頼度?安心度?を高めることができます。
(当然ながら、単なる数字の上の話なので、実際にはどうなのかは、やってみなければわからない)
平均以外のアプローチ #
平均以外にも、Excelやスプレッドシートでできるアプローチがいくつもあります。ここではざっくり、4つ挙げておきます。
- 中央値、最頻値
- 分散、標準偏差
中央値、最頻値(MEDIAN、MODE) #
外れ値があって平均を大きく上げ下げするようなデータがあるときは、中央値や最頻値を出しておくと、データの傾向をつかみやすくなります。中央値は、ソート済みの全データを2分した場所の値。最頻値は、読んで字のごとく、最も多く出現する値のこと。
下の画像は、とあるバッチの実行時間の平均、分散、標準偏差、中央値、最頻値を求めたものです。時間を扱うときは、単位を秒に変換すると便利ですが、変換しなくても計算はできます。
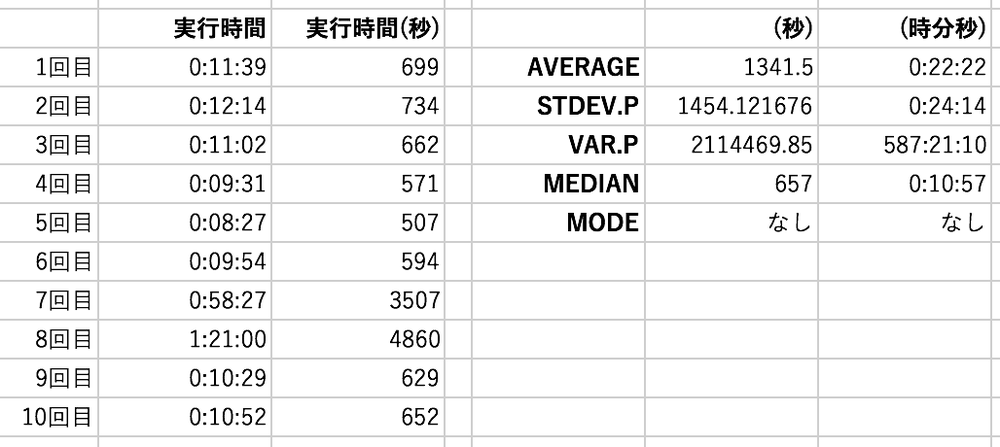
秒に変換してから計算するとやりやすい
↑7回目と8回目のデータが、平均(AVERAGE)に大きく影響しています。一方で、中央値(MEDIAN)は全体の傾向をうまく表せています。ばらつきの大きいデータのため、分散(VAR.P)、標準偏差(STDEV.P)が大きな値になりました。
※ 全体のデータから最大値・最小値を取り除いたデータで分析にかけることもあるようです(データのばらつきを抑えることができる)
分散、標準偏差(VAR、STDEV) #
これらの数字は見てもピンとこないし、普段は使いません。もっとも、これらの値の使いみちは、「あるデータは、全体の中でどれくらいの位置にいるのか(いわゆる偏差値)」を知るときに使うわけですがここでは扱いません。
※得られた数字がよく出てくる数字なのか、はたまためったに出現しなさそうな値なのかを調べるときに使えます。
推計 #
データは取ったし、平均も出たけど、いまいち心もとないときには、区間推定が役に立ちます。これさえ覚えておけば、だいぶ統計っぽくなります。
95%の信頼区間で推計します。この95%というのは統計では「ほとんど確実にそうなりそうといえる」という意味になるそうです。
母平均が95%の確率で取りうる範囲の推計 #
何回か試行をやってみた結果から、さらにデータが増えていったときの平均(母平均)の範囲を推計することができるそうです。「平均値はこの範囲に収まるっぽい」と言えるみたいです。
わかりにくいですが、**[データ範囲]**のところだけ書き換えればOK。
(上限)
=AVERAGE([データ範囲]) + TINV(0.05, COUNTA([データ範囲])-1) * SQRT(VAR([データ範囲]) / COUNTA([データ範囲]))
(下限)
=AVERAGE([データ範囲]) - TINV(0.05, COUNTA([データ範囲])-1) * SQRT(VAR([データ範囲]) / COUNTA([データ範囲]))
面倒なことは考えず、平均とTINV(0.05, COUNTA([データ範囲])-1) * SQRT(VAR([データ範囲]) / COUNTA([データ範囲]))だけ計算しておきます。あとはこの2つを ± で繋いであげればOK。
スクショをサンプルとして載せておきますが、下のような結果が出てきます。(上で挙げたデータ例とは異なります)


バッチの実行時間や、データサイズの傾向を示すことができるようになります。
データの95%が取りうる範囲の推計 #
とりあえずデータをとって、95%のデータがこの範囲に収まる、というのを計算したい場合は以下の式が使えます。**[データ範囲]**のところだけExcelやスプレッドシートで置き換えればOK。(データを母集団としたときの場合)
※ 以下の式が合っているのかは、ちょっと不安がある。本には書いてあったけど。
(上限)
=AVERAGE([データ範囲]) + 1.96 * STDEVP([データ範囲])
(下限)
=AVERAGE([データ範囲]) - 1.96 * STDEVP([データ範囲])
上の範囲に収まりそう、といえるらしいです。
1.96がなんなのかは、これといって覚える必要はありません。
もう少しわかりやすい表現を言うと、平均 ± 1.96×標準偏差の範囲にデータの95%が存在するということのようです。つまり、平均と1.96 * STDEVP([データ範囲])を計算しておけばOK。
分析に必要なデータの個数は… #
母平均を推定する手法では TINV という関数を用いて、分析に使うデータの個数を考慮した計算をするようにしてあります(データが少ないときは、推定範囲が広がるようになっている)。しかしながら、サンプルは多い方が推定の精度が高まります。
TINVの値は、95%の信頼区間(有意水準 0.05)のとき、自由度(サンプルの数 - 1)の値が大きくなるに連れて、1.96に近づいていきます(実際には1.959…)
| 自由度(n-1) | TINV(0.05, 自由度) |
|---|---|
| 1 | 12.71 |
| 2 | 4.30 |
| 3 | 3.18 |
| 4 | 2.78 |
| 5 | 2.57 |
| 10 | 2.23 |
| 20 | 2.09 |
| 30 | 2.04 |
| 40 | 2.02 |
| 50 | 2.01 |
| 80 | 1.99 |
| 100 | 1.98 |
| 200 | 1.97 |
| 500 | 1.96 |
少なくともサンプルは5個あると安心かなと(でもまだ安心ではない)。
しきい値を2.0で考えると、だいたい60〜70個くらいデータのサンプルがあると、だいぶいい感じの分析になるのかなぁと思います。確実な精度を求めるのであれば、501個以上で頑張るのが良さそうです。
そんなわけで、たまには平均以外も使えるようになると、統計っぽいことができて、いい感じのデータができるかなと思います。